STL – 1

Шаблоны

Мотивация

Рассмотренные в прошлых разделах перегрузки функций часто мало отличаются своим поведением, только типами, которые они принимают. В частности, рассмотрим функцию isGreater(a, b) от двух аргументов, которая должна возвращать true, если a > b, иначе – false

#include <iostream>

bool isGreater(int a, int b) {
    return a > b;
}

int main() {
    int a_1 = 2;
    int b_1 = 1;
    std::cout << "int, isGreater(a, b): " << isGreater(a_1, b_1) << '\n';

    double a_2 = 1.9;
    double b_2 = 1.1;
    std::cout << "double, isGreater(a, b): " << isGreater(a_2, b_2) << '\n';
}

int, isGreater(a, b): 1
double, isGreater(a, b): 0

При каждом вызове функции компилятор пытается определить, какая из объявленных функций подходит лучше всего для количества и типов аргументов. Если определить приемлемую функцию не удается, то произойдет ошибка компиляции.

В примере выше в обоих случаях будет вызвана функция bool isGreater(int a, int b), причем во втором случае произойдет неявное преобразование типов: double→ int, что и приведет к ошибке в выводе – будет опущена дробная часть вещественного числа

Исправим эту ошибку, добавив перегрузку для функции isGreater и аргументов типа double:

#include <iostream>

bool isGreater(int a, int b) {
    return a > b;
}

bool isGreater(double a, double b) {
    return a > b;
}

int main() {
    int a_1 = 2;
    int b_1 = 1;
    std::cout << "int, isGreater(a, b): " << isGreater(a_1, b_1) << '\n';

    double a_2 = 1.9;
    double b_2 = 1.1;
    std::cout << "double, isGreater(a, b): " << isGreater(a_2, b_2) << '\n';
}

int, isGreater(a, b): 1
double, isGreater(a, b): 1

Теперь вывод программы верный: действительно, во втором случае будет выбрана идельно подходящая функция для аргументов типа double: bool isGreater(double a, double b)

Почему это неудобно:

1. нам пришлось явно писать 2 перегрузки для разных типов

2. часто нужно еще больше перегрузок, например, для строк, что потребует еще больше времени для написания кода и уменьшит его читаемость

С++ предоставляет способ решения этой проблемы: возможно унифицировать работы с разными типа, если использовать шаблоны.

Например, вот 2 примера идентичного кода:

#include <iostream>
#include <string>

bool isGreater(int a, int b) {
    return a > b;
}

bool isGreater(double a, double b) {
    return a > b;
}

bool isGreater(const std::string& a, const std::string& b) {
    return a > b;
}

int main() {
    int a_1 = 2;
    int b_1 = 1;
    std::cout << "int, isGreater(a, b): " << isGreater(a_1, b_1) << '\n';

    double a_2 = 1.9;
    double b_2 = 1.1;
    std::cout << "double, isGreater(a, b): " << isGreater(a_2, b_2) << '\n';

    std::string a_3 = "abb";
    std::string b_3 = "aba";
    std::cout << "string, isGreater(a, b): " << isGreater(a_3, b_3) << '\n';
}

И с использованием шаблона типа:

#include <iostream>
#include <string>

template <typename T>
bool isGreater(const T& a, const T& b) {
    return a > b;
}

int main() {
    int a_1 = 2;
    int b_1 = 1;
    std::cout << "int, isGreater(a, b): " << isGreater(a_1, b_1) << '\n';

    double a_2 = 1.9;
    double b_2 = 1.1;
    std::cout << "double, isGreater(a, b): " << isGreater(a_2, b_2) << '\n';

    std::string a_3 = "abb";
    std::string b_3 = "aba";
    std::cout << "string, isGreater(a, b): " << isGreater(a_3, b_3) << '\n';
}

Оба примера произведут одинаковый вывод:

int, isGreater(a, b): 1
double, isGreater(a, b): 1
string, isGreater(a, b): 1

На самом деле на этапе компиляции из шаблона будут автоматически созданы необходимые перегрузки: чем бОльшим количеством типов будет вызываться функция, тем бОльшее количество перегрузок будет создано из шаблона.

То есть шаблон пишется перед функцией, структурой, классом, в нем определяем необходимое количество названий для типов, которые будет определены на этапе компиляции. Значит, с шаблонными типа неоходимо работать так, чтобы код был допустим для всех возможных типов. Например, в примере выше мы использовали только оператор сравнения, который определен как для чисел, так и для строк. С умножением на число в шаблонной функции последние примеры уже бы не скомпилировались

Где мы уже использовали шаблоны?

На самом деле в курсе уже не раз мы использовали шаблоны: шаблоанные типы указываются в фиксированном порядке в треугольных скобках после названия типа или функции (<>). Например: std::vector<T>, std::functional<F>, где вместо T и Fбыли подставлены желаемые типы элемента вектора и лямба-функции соответственно.

Так мы явно определяли шаблонный тип. В примерах выше определение шаблонного типа происходило неявно, компилятор его выводил (deduce) из предоставленного кода.

Если неявный вывод невозможен, тогда будет ошибка компиляции вроде “unable to deduce types for template structure/function/class”

Также неявный вывод мы использовали при использовании математических функций из хэдера <cmath>.

• Дисклеймер: Возможны реализации хэдеров без шаблонов…, но

  Возможны реализации хэдеров без шаблонов по разным причинам (совместимости, например), но суть остается той же, для простоты будем считать, что там используются шаблону

#include <iostream>
#include <iomanip>
#include <cmath>

int main() {
    double num;
    std::cin >> num;
    std::cout << std::fixed << std::setprecision(9) <<
    std::sqrt(num) << '\n' << sqrt(num) << '\n';
}

1. При подключении хэдера <cmath> функции вовсе не обязательно окажутся в глобальной области видимости, тогда std::sqrt и sqrt могут быть разными функциями.

2. Если это так, то потенциально может воспроизвестись ошибка, показанная в первых примерах, если sqrt написана только для целых чисел или считаем квадратный корень с меньшей точностью

STL – Standard template library

Это часть стандартной библиотеки C++, которая предоставляет доступ к готовым реализациям:

• контейнеров – std::vector, std::array, std::list, std::stack, std::queue, std::map

• итераторов

• алгоритмов – std::sort, std::swap, std::accumulate, std::reverse, std::fill, std::find, std::max_element, std::count

• функторы и операторы – арифметические и бинарные унарные и бинарные операторы, например. Функтор – объект, который можно вызвать как функцию: Functor(...)

В это разделе мы рассмотрим подробнее итераторы и ассоциативные контейнеры.

Итератор

Это объект, который указывает на некоторый элемент в контейнере. По своим возможностям он чем-то напоминает указатель, но обладает более широким и понятным функционалом.

Итератор всегда привязан к типу контейнера и, как следует из названия, предназначен для итерирования по нему. Тип итератора можно получить из типа контейнера.

В следующем примере создадим вектор целых чисел, а затем отсортируем его и выведем:

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::vector<int> v = {5, 2, 4, 1, 3};

    std::vector<int>::iterator it_begin = v.begin();
    std::vector<int>::iterator it_end = v.end();
    std::sort(it_begin, it_end); // std::sort(v.begin(), v.end());
    for (int elem : v) {
        std::cout << elem << " ";
    }
    std::cout << '\n';

    std::cout << *it_begin << ' ' << *(it_end - 1) << '\n';
}

1 2 3 4 5
1 5

В примере выше стоит обратить внимание на следующие моменты:

• тип итератора по вектору мы получаем из типа вектора: std::vector<int>::iterator

• v.begin() и v.end() – методы, которыми мы ранее пользовались – на самом деле возвращают итераторы на первый элемент и на память после последнего элемента соответственно

• как и указатель, итератор можно разыменовать – получить значение элемента, на который итератор указывает

• как и указатель, с итератором выполнять сложение и вычитание с числом, чтобы перейти к следующему и предыдущему элементу

• разность итераторов равна размеру вектора: it_end - it_begin == v.size() == 5

Более того, range-based for на самом деле работает именно на итераторах, вот эквивалентные циклы

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::vector<int> v = {5, 2, 4, 1, 3};

    for (int& elem : v) {
        elem *= 2;
        std::cout << elem << " ";
    }
    std::cout << '\n';
    std::cout << (v == std::vector<int>{10, 4, 8, 2, 6}) << '\n';
}

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::vector<int> v = {5, 2, 4, 1, 3};

    for (std::vector<int>::iterator it = v.begin(); it != v.end(); ++it) {
        *it *= 2;
        std::cout << *it << " ";
    }
    std::cout << '\n';
    std::cout << (v == std::vector<int>{10, 4, 8, 2, 6}) << '\n';
}

Вывод обеих программ совпадет:

10 4 8 2 6
1

Итераторы будут необходимы для понимания работы с контейнерами, которые будут рассмотрены далее.

Неупорядоченное множество (std::unordered_set<Key, Hash, KeyEqual>)

За определение множества возьмем один из варинтов в математике: множество – это неупорядоченный набор уникальных элементов.

В STL C++ std::unordered_set– это такой контейнер, который может хранить в себе уникальные элементы, причем предоставляет следующие операции со следующей асимптотической сложностью:

• добавление элемента – \({\cal{O}}(1)\)

• удаление элемента – \({\cal{O}}(1)\)

• проверка элемента на принадлежность std::unordered_set – \({\cal{O}}(1)\)

• итерирование итератором 😎 – \({\cal{O}}(n)\)

• аналогично вектору, константная сложность не точная, а амортизированная. В худшем случае (при нехватке выделенной памяти) сложность составит \({\cal{O}}(n)\)

Когда следует использовать неупорядоченное множество std::unordered_set?

• когда важно лишь наличие элементов, без их порядка

• интресует максимально быстрая проверка на принадлежность объекта к набору (ведь такая проверка будет проведена за \({\cal{O}}(1)\)!)

(Обзорно) Как достигаются такие сложности?

• объекты различаем по хэшу Hash (\({\cal{O}}(1)\)) и добавляем/ищем сразу в подконтейнере из всех элементов с конкретным значение хэша

• если в подконтейнере (“bucket”) несколько элементов (у них одинаковый хэш), то идем за линию и честно проверяем на равенство за \({\cal{O}}(s)\), где \(s\) – длина подконтейнера, очень малое число. Подконтейнер, как правило, является двусвязным (односвязным списком)

Честная линейная сложность может достигаться при:

• атаке на хэш-функцию: подбираем множество элементов с одинаковыми хэшами и добавляем в множество, что приводит к переполнению подконтейнеров. Тогда либо линейный проход по подконтейнеру дает “настоящую” линейную сложность, либо это приводит переаллокации элементов с теми же последствиями

• переполнении подконтейнеров, либо самого множества из подконтейнеров: аллокация памяти с возможным переносом элементов также обладает линейной сложностью

2 иллюстрации немного разных реализаций неупорядоченного множества. Чем они отличаются по своему устройству? Что у них общего?

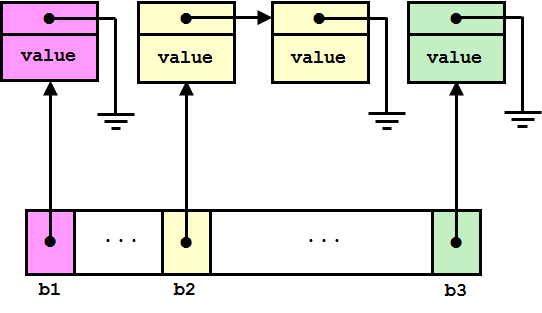
Источник и аналогичное объяснение

Источник и аналогичное объяснение

Источник картинки и исчерпывающее объяснение концепции

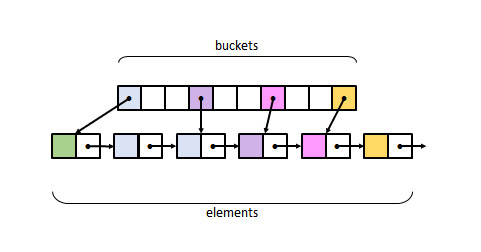
Источник картинки и исчерпывающее объяснение концепции

---

Все способы использования std::unordered_set:

#include <iostream>
#include <tuple>
#include <algorithm>
#include <vector>
#include <unordered_set>

int main() {
    // Creating
    std::unordered_set<int> uset1;                    // Default constructor
    std::unordered_set<int> uset2 = {1, 2, 3, 4, 5};  // Initializer list
    std::unordered_set<int> uset3 = uset2;            // Copy constructor

    // Modifying
    uset1.insert(10);            // Insert an element
    uset1.insert({20, 30, 40});  // Insert multiple elements
    uset1.erase(10);             // Erase an element by value
    uset1.erase(uset1.begin());  // Erase an element by iterator
    uset1.clear();               // Clear all elements

    // Accessing elements
    if (uset2.find(3) != uset2.end()) {
        std::cout << "Element 3 found in uset2" << '\n';
    }

    for (const int& elem : uset2) {
        std::cout << elem << ' ';
    }
    std::cout << '\n';

    // Checking size and properties
    std::cout << "Size of uset2: " << uset2.size() << '\n';
    std::cout << "Is uset3 empty? " << (uset2.empty() ? "Yes" : "No") << '\n';
}

Element 3 found in uset2
5 4 3 2 1
Size of uset2: 5
Is uset2s empty? No

Пример использования std::unordered_set<T>, где \(n\) целых чисел добавляют в неупорядоченное множество, а затем программ отвечает на \(m\) запросов: “принадлежит ли очередное введенное число множеству?”

Какова сложность этого алгоритма? Почему?

#include <iostream>
#include <algorithm>
#include <unordered_set>

int main() {
    std::unordered_set<int> data;
    size_t n;
    std::cin >> n;
    for (size_t i = 0; i < n; ++i) {
        int value;
        std::cin >> value;
        data.insert(value);  // O(1)
    }
    std::cout << "Data size: " << data.size() << '\n';

    for (std::unordered_set<int>::const_iterator it = data.begin(); it != data.end(); ++it) {
        std::cout << *it << ' ';
    }
    std::cout << '\n';

    size_t m;
    std::cin >> m;
    for (size_t i = 0; i < m; ++i) {
        int value;
        std::cin >> value;
        if (data.find(value) != data.end())  // O(1)
        {
            std::cout << "YES" << '\n';
        } else {
            std::cout << "NO" << '\n';
        }
    }
}

5
1 1 1 2 3
Data size: 3
3 2 1
4
1
YES
2
YES
3
YES
7
NO

Стоит обратить внимание на:

• отмеченные константные сложности добавления и поиска элемента

• вывод всех элементов написан с использованием итератора. Точнее, итератора на константные элементы – аналог константной ссылки. Изменить с помощью такого указателя элемент – невозможно. В чем разница между const std::unordered_set<int>::iterator и std::unordered_set<int>::const_iterator? Какие операции невозможны с каждым из этих типов? А какие – возможны?

• чтобы определить, есть ли элемент в множестве, нужно попробовать его найти с помощью метода std::set<T>::find(const T& elem). Этот метод возвращает итератор: на найденный элемент, если он все же есть в множестве, на конце множества (std::set<T>::end()), если элемент не был найден. Значит, условие data.find(value) != data.end() равносильно “если элемент был найден”, то есть “если метод find вернул НЕ конец множества”

• при добавлении в множество уже существующего там элемента ничего не происходит

• порядок в непорядоченном множестве действительно неопределен: обратите внимание на выведенные элементы множества

Упорядоченное множество (std::set<Key, Compare>)

Название говорит само за себя – элементы уникальные и хранятся в некотором порядке. (Реализовано на красно-черном дереве)

• добавление элемента – \({\cal{O}}(\log n)\)

• удаление элемента – \({\cal{O}}(\log n)\)

• проверка элемента на принадлежность std::set – \({\cal{O}}(\log n)\)

• итерирование итератором 😎 – \({\cal{O}}(n)\)

• в худшем случае (при нехватке выделенной памяти) сложность составит \({\cal{O}}(n)\)

Когда следует использовать неупорядоченное множество std::set?

• интересен порядок элементов по мере их добавления

• когда важно наличие элементов, порядок также требуется

Как быстрее получить упорядоченный набор из \(n\) объектов: добавить в вектор и отсортировать(сложность \(O(n \log n)\)) ИЛИ \(n\) раз добавить в std::set? Почему?

Пример работы с упорядоченным множеством:

#include <iostream>
#include <algorithm>
#include <set>

int main() {
    std::set<int> data;
    size_t n;
    std::cin >> n;
    for (size_t i = 0; i < n; ++i) {
        int value;
        std::cin >> value;
        data.insert(value);  // O(log n)
    }
    std::cout << "Data size: " << data.size() << '\n';

    for (std::set<int>::const_iterator it = data.begin(); it != data.end(); ++it) {
        std::cout << *it << ' ';
    }
    std::cout << '\n';
}

10
1 1 1 6 6 6 3 3 3 2
Data size: 4
1 2 3 6

Пара std::pair<T1, T2>

Пара – составной тип, который состоит из двух переменных разных типов.

Все способы создания, модификации и использования пар:

#include <iostream>
#include <tuple>
#include <algorithm>
#include <vector>
#include <string>

int main() {
    // Creating std::pair
    std::pair<int, std::string> p1(1, "one");
    std::pair<int, std::string> p2 = std::make_pair(2, "two");
    std::pair<int, std::string> p3{3, "three"};

    // Accessing elements
    std::cout << "p1: " << p1.first << ", " << p1.second << '\n';
    std::cout << "p2: " << p2.first << ", " << p2.second << '\n';
    std::cout << "p3: " << p3.first << ", " << p3.second << '\n';

    // Modifying elements
    p1.first = 10;
    p1.second = "ten";
    std::cout << "Modified p1: " << p1.first << ", " << p1.second << '\n';

    // Comparing pairs
    if (p1 < p2) {
        std::cout << "p1 is less than p2" << '\n';
    } else {
        std::cout << "p1 is not less than p2" << '\n';
    }

    // Swapping pairs
    std::swap(p1, p2);
    std::cout << "After swap, p1: " << p1.first << ", " << p1.second << '\n';
    std::cout << "After swap, p2: " << p2.first << ", " << p2.second << '\n';

    // Using pairs in a vector
    std::vector<std::pair<int, std::string>> vec;
    vec.push_back(p1);
    vec.push_back(p2);
    vec.push_back(p3);

    // Iterating over vector of pairs
    for (const auto& p : vec) {
        std::cout << "Vector element: " << p.first << ", " << p.second << '\n';
    }
}

p1: 1, one
p2: 2, two
p3: 3, three
Modified p1: 10, ten
p1 is not less than p2
After swap, p1: 2, two
After swap, p2: 10, ten
Vector element: 2, two
Vector element: 10, ten
Vector element: 3, three

Пример создания и поиска пар:

#include <iostream>
#include <tuple>
#include <vector>
#include <algorithm>

int main() {
    std::vector<std::pair<int, int>> pairs;
    int a, b;
    std::cout << "Enter pairs of integers (0 0 to stop): ";
    while (std::cin >> a >> b && (a != 0 || b != 0)) {
        pairs.push_back(std::make_pair(a, b));
    }

    std::cout << "First pair: " << pairs[0].first << " " << pairs[0].second << '\n';

    std::pair<int, int> find;
    std::cout << "Enter pair to find: ";
    std::cin >> find.first >> find.second;

    std::vector<std::pair<int, int>>::iterator found_iter = std::find(pairs.begin(), pairs.end(), find);
    // auto found_iter = std::find(pairs.begin(), pairs.end(), find);

    if (found_iter != pairs.end()) {
        std::cout << "Pair found: " << found_iter->first << " " << found_iter->second << '\n';
    } else {
        std::cout << "Pair not found" << '\n';
    }
}

Enter pairs of integers (0 0 to stop): 1 2
2 3
3 2
4 5
0 0
First pair: 1 2
Enter pair to find: 3 2
Pair found: 3 2

Ассоциативный контейнер std::unordered_map<Key, Value, Hash, KeyEqual>

#include <iostream>
#include <unordered_map>
#include <string>

bool isPositive(const std::string& key, const std::unordered_map<std::string, int>& data) {
    return data.at(key) > 0;
    // return data[key] > 0; Compilation Error due to !constant! argument data
}

int main() {
    std::unordered_map<std::string, int> data;
    std::string key;
    int value;

    while (std::cin >> key >> value) {
        data[key] = value;  // вставка
    }

    data.erase("hello");  // удаление

    // поиск
    auto iter = data.find("test");
    if (iter != data.end()) {
        std::cout << "Found the key " << iter->first << " with the value " << iter->second << "\n";
    } else {
        std::cout << "Not found\n";
    }
}