Алгоритмы сортировки

В этой главе нам предстоит формально определить сортировку элементов, обосновать нижнюю оценку на асимптотику и разобрать несколько алгоритмов сортировки, которые нужно будет самостоятельно реализовать.

Если не указано иное, то мы рассматривание объекты, для которых определен только оператор “меньше”. Это значит, чзто, имея \(a_1\) и \(a_2\), мы можно только определить истинности выражения \(a_1 < a_2\).

Сортировка – это процесс поиска такого расположения объектов, для которого будет выполняться введенное отношения порядка (\(\forall i < j \ : \ a_i < a_j\)). Формально сортировка – это поиск такой перестановки индексов, что \(a_{p_1} < a_{p_2} < ... < a_{p_n}\), где \(p\) – это перестановка индексов от 1 до n. Это наблюдение пригодится нам при доказательстве нижней оценки сложности алгоритмов сортировки.

Квадратичные сортировки

Сортировка пузырьком

Сортировка пузырьком – это алгоритм, который проходит по массиву и сравнивает соседние элементы. Если текущий элемент больше следующего, то они меняются местами. Алгоритм повторяет эту процедуру до тех пор, пока массив не будет отсортирован.

Допустим, у нас есть массив \([5, 3, 8, 4, 2]\).

Шаг	Описание	Массив
1	Сравниваем 5 и 3. Поскольку 5 > 3, меняем их местами	\([3, 5, 8, 4, 2]\)
2	Сравниваем 5 и 8. Поскольку 5 < 8, ничего не меняем	\([3, 5, 8, 4, 2]\)
3	Сравниваем 8 и 4. Поскольку 8 > 4, меняем их местами	\([3, 5, 4, 8, 2]\)
4	Сравниваем 8 и 2. Поскольку 8 > 2, меняем их местами	\([3, 5, 4, 2, 8]\)
5	Повторяем процесс для всего массива	-

В результате мы получаем отсортированный массив: \([2, 3, 4, 5, 8]\).

Важно понять, как и почему такой алгоритм действительно работает. Заметим, что на каждой итерации алгоритм “выталкивает” наибольший элемент в конец массива. Действительно, ведь такой элемент сможет “победить” во всех сравнениях с любым соседом, поэтому после его нахождения он начнет “всплывать” в конец массива. Таким образом, после первой итерации наибольший элемент оказывается в последней позиции, после второй итерации – на предпоследней и так далее. Это приводит к тому, что после \(i\)-той итераций последние \(i\) элементов массива уже отсортированы, значит, после \(n\) итераций массив будет отсортирован полностью.

Алгоритм (псевдокод)

function bubble_sort(arr):
    n -- длина массива
    arr -- массив, который нужно отсортировать
    делаем n шагов
    для i от 0 до n-1:
        делаем n-i-1 шагов
        для j от 0 до n-i-2:
            если arr[j] > arr[j+1]:
                меняем местами arr[j] и arr[j+1]
    возвращаем arr

Сложность такого алгоритма составляет:

\[ {\cal{O}(n^2)} \]

Сортировка выбором

Сортировка выбором – это алгоритм, который проходит по массиву и находит минимальный элемент. Затем он меняет его местами с первым элементом массива. После этого алгоритм повторяет процесс для оставшейся части массива. Этот алгоритм работает аналогично сортировке пузырьком, но вместо того, чтобы “выталкивать” элементы, он “выбирает” минимальный элемент и помещает его на нужную позицию. Очевидно, что после \(n\) итераций массив будет отсортирован полностью.

Допустим, у нас есть массив \([5, 3, 8, 4, 2]\).

Шаг	Описание	Массив
1	Находим минимальный элемент (2) и меняем его местами с первым элементом (5)	\([2, 3, 8, 4, 5]\)
2	Находим минимальный элемент (3) и меняем его местами со вторым элементом (3)	\([2, 3, 8, 4, 5]\)
3	Находим минимальный элемент (4) и меняем его местами с третьим элементом (8)	\([2, 3, 4, 8, 5]\)
4	Находим минимальный элемент (5) и меняем его местами с четвертым элементом (8)	\([2, 3, 4, 5, 8]\)

В результате мы получаем отсортированный массив: \([2, 3, 4, 5, 8]\).

Алгоритм (псевдокод)

function selection_sort(arr):
    n -- длина массива
    arr -- массив, который нужно отсортировать
    делаем n шагов
    для i от 0 до n-1:
        # находим индекс минимального элемента в оставшейся части массива
        min_index = argmin(arr[i, i+1, i+2, ..., n-1])

        меняем местами arr[i] и arr[min_index]
    возвращаем arr

Сложность такого алгоритма составляет:

\[ {\cal{O}(n^2)} \]

Сортировка вставками

Сортировка вставками – это алгоритм, который проходит по массиву и на каждой итерации берет один элемент и вставляет его в правильную позицию среди уже отсортированных элементов.

Сначала алгоритм считает, что первый элемент массива уже отсортирован. Затем он проходит по остальным элементам и вставляет их в правильную позицию среди уже отсортированных элементов. Делается это путем сравнения текущего элемента с предыдущими и сдвигая элементы, которые больше текущего, на одну позицию вправо.

Допустим, у нас есть массив \([5, 3, 8, 4, 2]\).

Шаг	Описание	Массив
1	Считаем, что первый элемент уже отсортирован	\([5]\)
2	Вставляем второй элемент (3) в правильную позицию	\([3, 5]\)
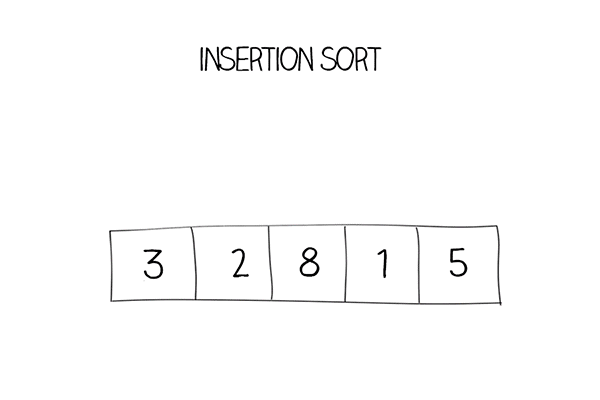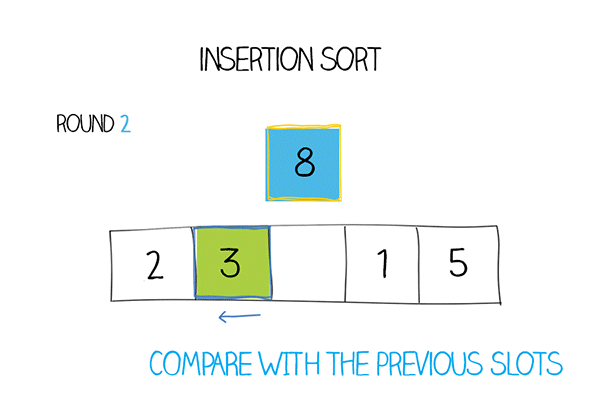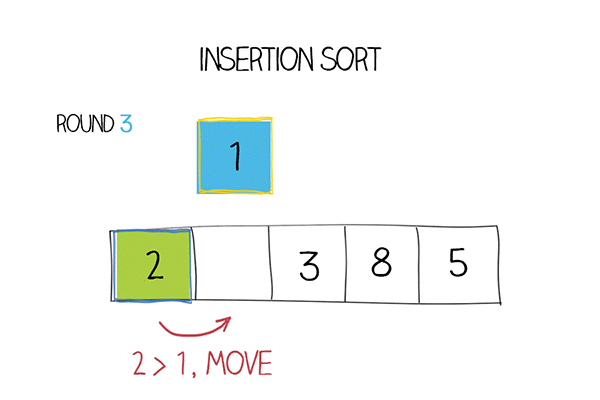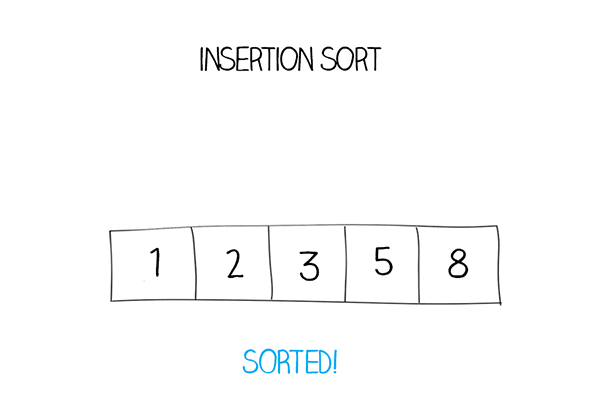
3	Вставляем третий элемент (8) в правильную позицию	\([3, 5, 8]\)
4	Вставляем четвертый элемент (4) в правильную позицию	\([3, 4, 5, 8]\)
5	Вставляем пятый элемент (2) в правильную позицию	\([2, 3, 4, 5, 8]\)

В результате мы получаем отсортированный массив: \([2, 3, 4, 5, 8]\).

Алгоритм (псевдокод)

function insertion_sort(arr):
    n -- длина массива
    arr -- массив, который нужно отсортировать
    делаем n шагов
    для i от 1 до n-1:
        key = arr[i]
        j = i - 1
        пока j >= 0 и arr[j] > key:
            arr[j + 1] = arr[j]
            j = j - 1
        arr[j + 1] = key
    возвращаем arr

Сложность такого алгоритма составляет:

\[ {\cal{O}(n^2)} \]

Оптимальные сортировки

Можно ли сделать сортировку быстрее, чем \({\cal{O}(n^2)}\)? Конечно.

Если у нас определена только операция “меньше”, то мы не можем обойтись без \({\cal{O}(n \log n)}\) операций. Докажем это.

Введем понятие дерева решений. Дерево решений – это бинарное дерево, в котором каждый узел представляет собой сравнение двух элементов массива. В каждом узле дерева находится подмножество множества всех перестановок на n элементов.

В корне дерева находится множество всех перестановок.
Каждый узел дерева представляет собой сравнение двух элементов массива. Если \(a_i < a_j\), то мы идем в левое поддерево, иначе – в правое. В корне левого поддерева находятся все перестановки, в которых \(a_i < a_j\), а в корне правого поддерева – все перестановки, в которых \(a_i > a_j\).
Каждый лист дерева представляет собой одну из возможных перестановок
Значит, в таком дереве будет \(n!\) листьев, так как у нас есть n элементов и \(n!\) возможных перестановок.
Поскольку дерево бинарное, то высота дерева будет равна \(\log_2(n!)\).

Оценим снизу высоту дерева:

\[ h = \log_2(n!) = \log_2 (n^n + \bar{o}(n^{n - 1})) \ge \log_2(n^n) = n \log_2(n) \]

Поскольку, высота дерева равна количеству сравнений, то мы получаем нижнюю оценку на сложность сортировки:

\[ \Omega \left( n \log_2(n) \right) \]

Сортировка слиянием (merge sort)

Сортировка слиянием – это алгоритм вида “разделяй и властвуй”, который разбивает массив на две половины до тех пор, пока каждая половина не станет размером в один элемент. Затем он объединяет эти половины обратно вместе в отсортированном порядке.

Введем вспомогательную операцию слияния двух отсортированных массивов. Эта операция принимает два отсортированных массива и объединяет их в один отсортированный массив. Это легко можно сделать, если создать два указателя, которые будут указывать на начало каждого массива. Затем мы будем сравнивать элементы, на которые указывают указатели, и добавлять меньший элемент в результирующий массив. После этого мы будем двигать указатель на массив, из которого был взят элемент. Когда один из массивов будет полностью обработан, мы просто добавим оставшиеся элементы другого массива в результирующий массив.

Алгоритм слияния (псевдокод)

function merge(arr1, arr2):
    merged = []
    i = 0
    j = 0
    пока i < len(arr1) И j < len(arr2):
        если arr1[i] < arr2[j]:
            merged.append(arr1[i])
            i += 1
        иначе:
            merged.append(arr2[j])
            j += 1
    добавляем оставшиеся элементы из arr1 и arr2 в merged, если они есть
    возвращаем merged

Далее будем работать по следующей схеме:

Мы разбиваем массив на две половины.
Мы рекурсивно сортируем каждую половину.
Мы объединяем отсортированные половины обратно вместе с помощью операции слияния.

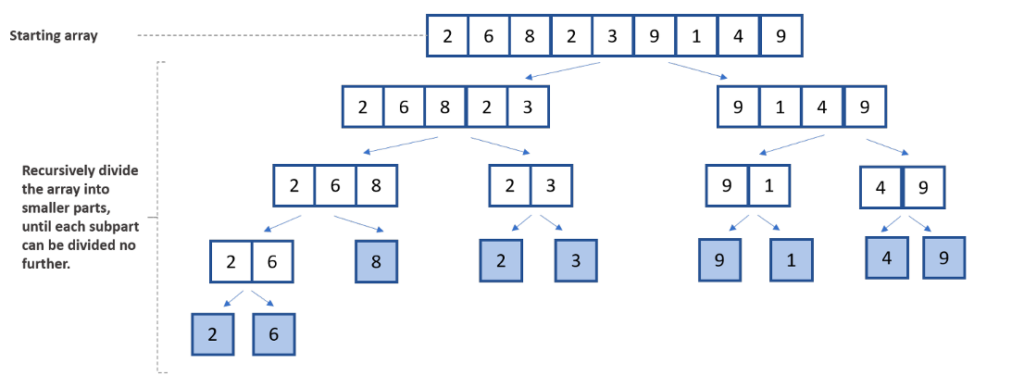
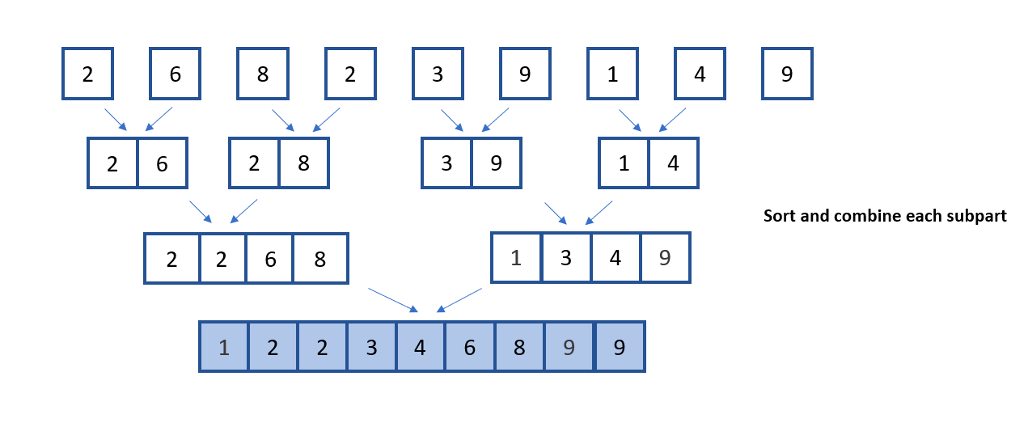
Алгоритм сортировки слиянием (псевдокод)

function merge_sort(arr):
    если длина arr <= 1:
        возвращаем arr
    mid = длина arr // 2
    левая_часть = merge_sort(arr[:mid])
    правая_часть = merge_sort(arr[mid:])
    возвращаем merge(левая_часть, правая_часть)

Заметим, что сложность операции слияния составляет \({\cal{O}(n)}\), так как мы проходим по всем элементам обоих массивов. Разбивать массив на две половины можно не более \(\log_2(n)\) раз.

Сложность такого алгоритма составляет:

\[ {\cal{O}(n \log n)} \]

Быстрая сортировка (quick sort)

Быстрая сортировка – это алгоритм вида “разделяй и властвуй”, который разбивает массив на две части на основе опорного элемента (pivot по-английски), где в левой половине хранятся элементы, меньше или равные опорному, а в правой – большие опорного. Операция такого разделения называется partition. Затем алгоритм быстрой сортировки рекурсивно сортирует каждую из частей.

Алгоритм partition (псевдокод)

функция partition(arr, l, r):
    v = arr[(l + r) // 2]
    i = l
    j = r
    пока i ≤ j:
        пока arr[i] < v:
            i = i + 1
        пока arr[j] > v:
            j = j - 1
        если i ≥ j:
            break
        поменять местами arr[i] и arr[j]
        i = i + 1
        j = j - 1
    вернуть j

Этот алгоритм работает следующим образом:

Мы выбираем опорный элемент
Идем с начала массва до тех пор, пока не найдем элемент, который больше опорного
Идем с конца массива до тех пор, пока не найдем элемент, который меньше опорного
Найденный элементы стоят не на своих местах, поэтому мы меняем их местами
Повторяем шаги 2-4 до тех пор, пока не дойдем до середины массива

После выполнения операции partition массив будет разбит на две части: элементы меньше или равные опорному и элементы больше опорного. Затем мы рекурсивно сортируем каждую из частей.

Алгоритм быстрой сортировки (псевдокод)

function quick_sort(a, l, r):
    если l < r:
        q = partition(a, l, r)
        quick_sort(a, l, q)
        quick_sort(a, q + 1, r)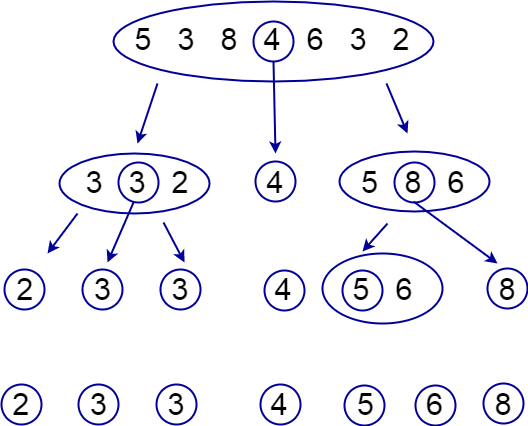

Сложность такого алгоритма в среднем составляет:

\[ {\cal{O}(n \log n)} \]

Важно отметить, что быстрая сортировка работает быстрее, чем сортировка слиянием, так как она использует меньше памяти. Это связано с тем, что быстрая сортировка работает на месте (in-place), то есть не требует дополнительной памяти для хранения промежуточных массивов.

Также можно понимать, что в худшем случае сложность быстрой сортировки составляет \({\cal{O}(n^2)}\), например, когда разбиение массива происходит неудачно и массив разбивается на две части, одна из которых содержит \(1\) элемент, а другая – \(n-1\) элементов. В этом случае быстрая сортировка будет работать так же, как сортировка выбором.

Интересно, что если способ выбора опорного элемента известен заранее, то всегда можно подобрать такой вход, что сложность сортировки будет квадратичной. Например, если мы всегда выбираем первый элемент массива в качестве опорного, то массив, отсортированный по убыванию, будет работать за \({\cal{O}(n^2)}\). В реальных задачах обычно используют случайный выбор опорного элемента, что позволяет избежать худшего случая.