Геометрия — 1
Отрезок, для которого указано, какой из его концов считается началом, а какой концом, называется вектором. Вектор на плоскости можно задать двумя числами — его координатами по горизонтали и вертикали.

Точка \(\simeq\) вектор. Так как оба задаются просто парой чисел, можно считать их одним и тем же классом объектов и сопоставлять каждой точке её радиус-вектор — вектор из начала координат, ведущий в эту точку.
Как их хранить
Создадим класс, который будет отвечать за все операции с векторами. В C++ есть два способа это сделать: через struct и через class. Их основное отличие в том, что по умолчанию в class все поля приватные — к ним нет прямого доступа снаружи. Это нужно для дополнительной защиты, чтобы в крупных проектах никто случайно ничего не поломал, но на олимпиадах это не очень актуально, поэтому объявим struct. По принятой в математике и физике нотации, назовём его r. Если хотите, можете назвать его point, pt, vec — как угодно.
struct r {
int x, y;
r() {}
r(int x, int y) : x(x), y(y) {}
};Функция r внутри класса или структуры с таким же именем вызывается при инициализации объекта. Её называют конструктором, и её можно указывать разную для разных входных аргументов. Здесь r()вернёт точку с неопределенными (какие оказались в памяти в тот момент) координатами, а r(x, y) вернет точку с координатами \((x, y)\).
Важным моментом является то, что мы выбрали целочисленный тип, int, для хранения координат. Если все входные координаты целые, то, как мы увидим, очень часто можно все операции тоже проводить в целых числах, что позволяет избежать многих проблем чисел с плавающей точкой.
Операции над векторами
Давайте напишем функцию, которая принимает вектор и что-то с ним делает. Например, считает длину:
double len(r a) { return sqrt(a.x * a.x + a.y * a.y); }
// или:
double len(r a) { return hypot(a.x, a.y); }Это подход языка C. В C++ удобнее определить метод:
double r::len() { return hypot(x, y); }
// (альтернативно можно добавить функцию len() внутри самой структуры)Помимо чуть более чистой реализации, есть ещё разница в синтаксисе вызова: len(a) или a.len().
Операторы
В C++ можно перегружать почти все стандартные операторы, например, +, -, * и т. д.
Переопределим для будущих нужд + и -:
r operator+(r a, r b) { return {a.x + b.x, a.y + b.y}; }
r operator-(r a, r b) { return {a.x - b.x, a.y - b.y}; }Как вы думаете, как на самом деле работает cin >> x? Это тоже перегрузка оператора: >>. Делается это так:
istream& operator>>(istream &in, r &p) {
in >> p.x >> p.y;
return in;
}
ostream& operator<<(ostream &out, r &p) {
out << p.x << " " << p.y << endl;
return out;
}Углы и повороты
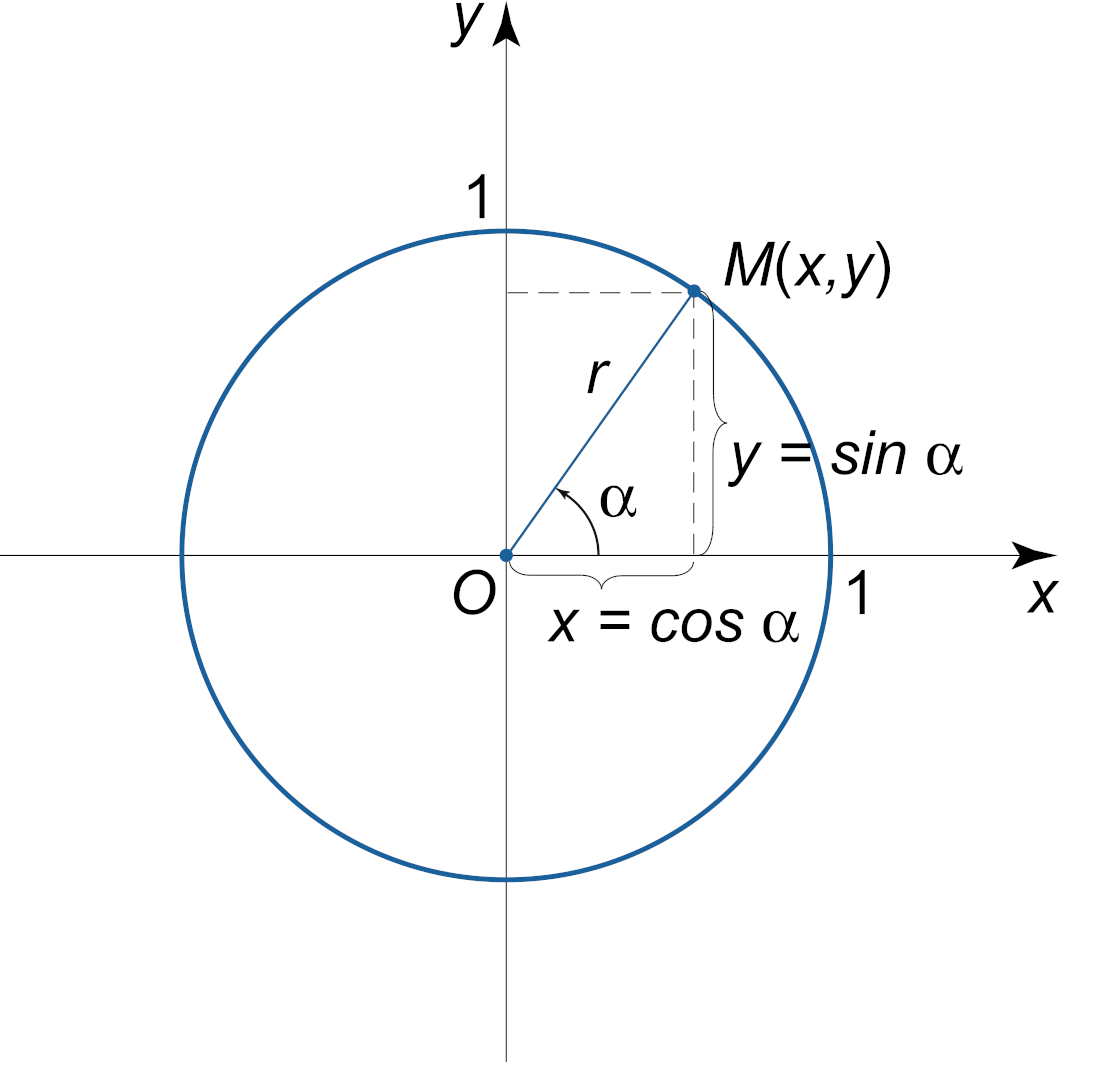
Для подсчета угла вектора относительно оси \(x\) можно вспомнить тригонометрический круг и посчитать арктангенс от \(\frac{y}{x}\).
В C++ и Python есть функция atan2, которая делает это немного быстрее и точнее деления и арктангенса:
double r::angle() {
return atan2(y, x);
}Вернется число от в промежутке \([-\pi, +\pi]\), в радианах. Для градусов нужно домножить на \(\frac{180}{\pi}\).
Помимо очевидных сложения, вычитания и умножения на константу, у векторов можно ввести и свои особенные операции, которые нам упростят жизнь.
Скалярное произведение
Скалярное произведение (англ. dot product) двух векторов равно произведению их длин и косинуса угла между ними. Для него справедлива следующая формула:
\[ a \cdot b = |a| \cdot |b| \cdot \cos \theta = x_a x_b + y_a y_b \]
Она доказывается муторно и чисто технически, так что мы это делать не будем.
Геометрически, она равна проекции вектора \(b\) на вектор \(a\), помноженный на длину \(а\):
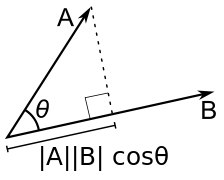
Полезные свойства:
Скалярное произведение симметрично (\(a \cdot b = b \cdot a\)).
Перпендикулярные вектора должны иметь нулевое скалярное произведение.
Если угол острый, то скалярное произведение положительное.
Если угол тупой, то скалярное произведение отрицательное.
Добавим в нашу реализацию отдельный оператор для него:
int operator*(r a, r b) { return a.x * b.x + a.y * b.y; }Векторное произведение
Векторное произведение (англ. cross product, также называется косым или псевдоскалярным) для двух векторов равно произведению их длин и синуса угла между ними — причём знак этого синуса зависит от порядка операндов. Оно тоже удобно выражается в координатах:
\[ a \times b = |a| \cdot |b| \cdot \sin \theta = x_a y_b - y_a x_b \]
Так же, как и со скалярным произведением, доказательство координатной формулы оставляется упражнением читателю. Если кто-то захочет это сделать: это следует из линейности обоих произведений (что в свою очередь тоже нужно доказать) и разложения по базисным векторам \(\overline{(0, 1)}\) и \(\overline{(1, 0)}\).
Геометрически, это ориентированная площадь параллелограмма, натянутого на вектора \(a\) и \(b\):

Его свойства:
Векторное произведение антисимметрично: \(a \times b = - (b \times a)\).
Коллинеарные вектора имеют нулевое векторное произведение.
Если \(b\) «слева» от \(a\), то векторное произведение положительное.
Если \(b\) «справа» от \(a\), то векторное произведение отрицательное.
Для него обычно тоже перегружают оператор — либо ^, либо %:
int operator^(r a, r b) { return a.x*b.y - b.x*a.y; }Примечание. Вообще говоря, формально векторное произведение определяется не так. Оно определено как вектор такой же длины, но перпендикулярный обоим исходным векторам. Это имеет применение в трёхмерной геометрии и физике, но пока в нашем двумерном мире об этом думать не надо.
Скалярное и векторное произведения тесно связаны с углами между векторами и могут использоваться для подсчета величин вроде ориентированных углов и площадей, которые обычно используются для разных проверок.
Когда они уже реализованы, использовать произведения гораздо проще, чем опираться на алгебру. Например, можно легко вычислить угол между двумя векторами, подставив в знакомый нам atan2 векторное и скалярное произведение:
double angle(r a, r b) {
return atan2(a ^ b, a * b);
}В дальнейшем, свойства произведений помогут нам в определении взаимного расположения точек и, например, прямой, поэтому важно эти свойства понять и крепко запомнить.
Прямые и отрезки
Отрезок можно задать двумя точками своих концов. В любом порядке — ведь он, в отличие от вектора, неориентирован.
struct segment {
r p, q;
};В вычислительной геометрии часто требуется уметь определять взаимное положение геометрических объектов. Например, проверять, пересекаются ли отрезки. В этом нам поможет скалярное и векторное произведение, а также небольшой разбор случаев:
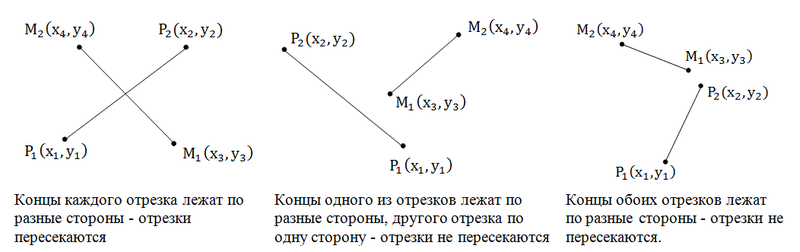
В терминах произведений, «концы отрезка лежат по разные стороны относительно другого отрезка», например, записывается как:
\[ [(M_1 - P_1) \times (P_2 - P_1)] \cdot [(M_2 - P_1) \times (P_2 - P_1)] < 0 \]
Записав ещё одно дополнительное условие, относительно \((M_1, M_2)\) в качестве разделительного отрезка, мы получим легко вычислимый предикат, который верен тогда и только тогда, когда отрезки пересекаются.
Лучи и прямые
Луч — это отрезок, бесконечный в одном из направлений. Его можно хранить как точку и либо явный вектор направления, либо любую другую его точку.
С прямыми дела обстоят немного сложнее. Здесь есть целых 4 имеющих право на жизнь способа их хранить:
Нормальным уравнением: \(A \cdot x + B \cdot y + C = 0\).
Двумя точками.
Точкой и направляющим вектором (любым): \(\vec{r} = \vec{a}t + \vec{b}\).
Точкой и нормальным вектором (любым).
Также их иногда удобно хранить уравнением \(y = kx + b\), как в школе, однако для вертикальных прямых придётся делать отдельный костыль.
Часто во входе прямые заданы в одном виде, но удобнее работать с другим. Реализуются основные переходы так:
\(2 \rightarrow 1\): достаточно найти любое решение системы из 2 уравнений и 3 неизвестных.
\(1 \rightarrow 3\): если прямая задаётся уравнением, то вектор \(\overline{(-B; A)}\) — направляющий к прямой (важно помнить, что у прямой есть два «направления»).
\(1 \rightarrow 4\): если прямая задаётся уравнением, то вектор \(\overline{(A; B)}\) — нормальный к прямой (важно помнить, что упрямой есть 2 «направления нормали»).
\(4,3 \rightarrow 1\): нужно решить систему из 1 уравнения и 1 неизвестного, раз уж из предыдущих пунктов мы уже знаем подходящие \(A\) и \(B\).
\(1 \rightarrow 2\): достаточно выбрать любые две точки на прямой — например:
// даны A, B, C (A^2 + B^2 != 0)
r a, b;
if (eq(A, 0)) // если это горизонтальная прямая
a = {0, -C/B}, b = {1, -C/B};
else
a = {-C/A, 0}, b = {-(C+B)/A, 1};Проверки
Для способов 2-4 все проверки почти такие же, как для отрезков. На самом деле, в геометрических задачах часто можно ввести «bounding box» — квадрат с очень далекими границами, все точки за пределами которого считаются «бесконечностью». Тогда бесконечные прямые и лучи можно заменить на отрезки, упирающиеся в эти бесконечные границы, и делать все проверки как с обычными отрезками.
В случае прямых, заданных формулой, всё совсем по-другому.
Расстояние от точки до прямой
Заметим, что если прямая задается уравнением вида \(Ax + By + C = 0\), то полуплоскость можно задать таким же неравенством. Это можно сразу использовать для проверки, по какую сторону от прямой находится точка.
Вектор нормали этой прямой будет иметь координаты \((A, B)\). Он перпендикулярен прямой, а в случае с полуплоскостью \(Ax + By + C \geq 0\) будет указывать в сторону самой полуплоскости.
Чтобы найти расстояние от точки \((x_0, y_0)\) до прямой \(Ax + By + C = 0\), можно воспользоваться следующей формулой:
\[ d = \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} \]
Об этой формуле можно думать как о скалярном произведении вектора-точки на нормированный (\(\frac{1}{\sqrt{A^2+B^2}}\)) вектор нормали, геометрически равный проекции точки на него.
Если же прямая задана 2 точками, то можно выразить высоту из формулы для площади треугольника:
\[ A = \frac{1}{2} bh \implies h = \frac{2A}{b} \]
И посчитать эту высоту так:
\[ \rho(P, L(A, B)) = \frac{|\overrightarrow{PA} \times \overrightarrow{PB}|}{|\overrightarrow{AB}|} \]
Обратите внимание, что в числителе стоит векторное произведение — мы воспользовались тем, что по модулю оно равно удвоенной площади треугольника \(\angle PAB\),
Точка пересечения прямых
Найти точку пересечения двух прямых — это то же самое, что и найти точку, которая удовлетворяет обоим условиям их уравнений:
\[ \begin{cases} A_1 x + B_1 y + C_1 = 0 \\ A_2 x + B_2 y + C_2 = 0 \end{cases} \]
Если выразить из обоих уравнений \(x\) и приравнять, то получается
\[ \begin{cases} -x = \frac{B_1 y + C_1}{A_1} \\ -x = \frac{B_2 y + C_2}{A_2} \end{cases} \implies \frac{B_1 y + C_1}{A_1} = \frac{B_2 y + C_2}{A_2} \implies y = - \frac{A_1 C_2 - A_2 C_1}{A_1 B_2 - A_2 B_1} \]
Аналогично, \(x = \frac{B_1 C_2 - B_2 C_1}{A_1 B_2 - A_2 B_1}\) (обратите внимание на знаки).
Заметим, что знаменатель может оказаться нулем. Это означает, что векторное произведение векторов нормали нулевое, а значит прямые параллельны — тогда точек пересечения либо нет, либо, в случае совпадающих прямых, бесконечность. Этот случай нужно обрабатывать отдельно.
Приведем несколько примеров конструктивного подхода.
Проекция точки на прямую
Чтобы спроецировать точку \(P\) на прямую \(L\), достаточно прибавить к ней нормальный вектор прямой, приведённый к длине \(\rho(P, L)\) и направленный от точки к прямой. Поскольку нормальный вектор может быть направлен в двух разных (но противоположных друг другу!) направлениях, то достаточно попробовать оба варианта, и принять тот, в котором расстояние от получившейся точки до прямой будет меньше.
Отражение от прямой
Пусть нам надо отразить точку \((x_0, y_0)\) симметрично относительно заданной прямой \(ax+by+c=0\).
Чисто в педагогических целях, начнём решать эту задачу как математики, чтобы никогда потом так не делать.
\[ \Pr_a b = \frac{a \cdot b}{|a|} \frac{a}{|a|} = \frac{|a| |b| \cos \alpha}{|a|} \frac{a}{|a|} = |b| \cos \alpha \frac{a}{|a|} \]
Геометрический смысл: длина на единичный вектор направления.
Мы не хотим раскрывать эти формулы покоординатно и предъявлять готовый ответ. Мы знаем, что он получится громоздким. Нам не жалко посчитать всё по частям — здесь нет смысла заниматься оптимизациями. Также мы хотим делать всё по частям, потому что так становится более наглядной логика алгоритма, и, как следствие, его проще дебажить.
// прямая r = at + b, точка c
r pr(r a, r b, r c) {
c -= b; // пусть c и a выходят из одной точки
return b + (a * b / len(a) / len(a)) * a;
}
r reflect(r a, r b, r c) {
return c + 2*(pr(a, b, c)-c);
}