Константность. Структуры

Константность

Константная переменная доступна только для чтения, ее изменение невозможно. Значение константной переменной должно быть зафиксировано в момент присваивания (то есть может быть неизвестно в момент компиляции)

Например:

#include <iostream>

int main() {
    // известна до компиляции (compile time)
    const int const_var_1 = 42;

    int number;
    std::cin >> number;
    // определяется только во время исполнения (run time)
    const int const_var_2 = 2 * number;

    const_var_1 += 1; // невозможно, будет ошибка компиляции

}

В первую очередь константность необходима для ясности программы: мы намеренно накладываем ограничение на использование переменной, что гарантировать ее неизменность в нашем коде, так и при вызове сторонних функций и методов.

Например, некоторые методы (которые его изменяют) константного вектора (const std::vector<T>) недоступны:

#include <iostream>
#include <vector>

int main() {
    const std::vector<int> v = {1, 3, 5};
    std::cout << v.size() << "\n"; // 3
    v.clear();  // nope: Compilation Error
    v[0] = 0;  // nope again: Compilation Error
}

Константные ссылки

Как известно, ссылка – это псевдоним переменной, который ведет себя ровно так же, как и “оригинал”. Теперь предстоит узнать, что можно создать псевдоним только для чтения – это и будет константная ссылка

int main() {
    int x = 42;

    int& ref = x;
    const int& const_ref = x;  // константная ссылка
    ++x;  // инкремент оригинала -- ОК
    ++ref;  // инкремент обычной ссылки -- ОК
    ++const_ref;  // изменение по константной ссылке невозможно -- CE
}

Наиболее это полезно в аргументах функции. Рассмотрим модифицированный пример из прошлой главы и объясним, почему в нем стоило использовать именно константную ссылку:

#include <iostream>
#include <string>

size_t countChar(const std::string& line, char chr_to_count) {
    size_t cnt = 0;
    for (const char& chr : line) {
        if (chr == chr_to_count) {
            ++cnt;
        }
    }
    return cnt;
}

int main() {
    std::string input_line;
    std::getline(std::cin, input_line);
    // мы уверены, что строке не будет изменена
    std::cout << countChar(input_line, 'a') << '\n';

    // было бы невозможно с неконстантной ссылкой: переменная константна
    const std::string const_line = "another constant line";
    std::cout << countChar(const_line, 'a') << '\n';

    // было бы невозможно с неконстантной ссылкой: переменной по факту нет
    std::cout << countChar("some random line with many aaaaa", 'a') << '\n';
}

Использование константной ссылки позволяет:

• расширить возможности для вызова функции: можно использовать константные переменные и литералы

• убедиться, что переменная нигде не изменится: иначе будет ошибка компиляции

• дать больше гарантий пользователям функций: уже по сигнатуре функции можно понять, какие переменные подлежат изменению, а какие – нет

Вложенные std::vector<T>

Вложенными векторами мы будем называть векторы из векторов, то есть объекты типа std::vector<std::vector<int>>. Это вектор, элементами которого являются векторы, а их элементами являются числа.

Например:

#include <iostream>
#include <vector>

int main() {
    const std::vector<std::vector<int>> data = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
    std::cout << data[0][0] << ' ' << data[1][1] << ' ' << data[2][2] << '\n';
    // 1 5 9
}

Так работает индексация в двумерном векторе:

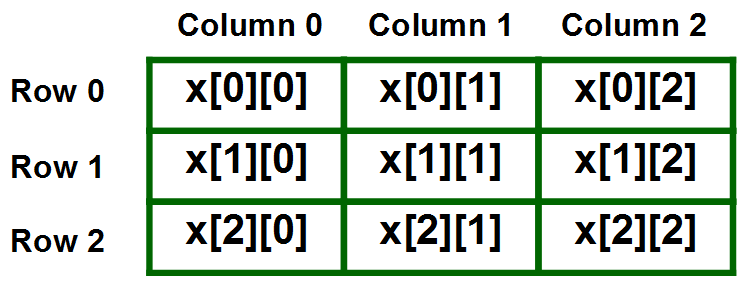Индексация в двумерном векторе: сначала получаем ряд, потом элемент в этом ряду

Двумерный вектор из примера выше

Создадим двумерный вектора и выведем его элементы. Затем выведем только его диагональ.

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    size_t m, n;
    std::cin >> m >> n;  // число строк и столбцов

    // создаём матрицу matrix из m строк
    std::vector<std::vector<int>> matrix(m);
    // std::vector<std::vector<int>> matrix(m, std::vector<int>(n));

    for (size_t i = 0; i < m; ++i) {
        matrix[i].resize(n);
        for (size_t j = 0; j < n; ++j) {
            std::cin >> matrix[i][j];
        }
    }
    // тип matrix[i] -- это std::vector<int> -- как и раньше,
    //переходим к элементу вектора по индексу

    // напечатаем матрицу, выводя элементы через табуляцию
    for (size_t i = 0; i < m; ++i) {
        for (size_t j = 0; j < n; ++j) {
            std::cout << matrix[i][j] << '\t'; // сначала индекс строки, затем индекс элемента в этой строке
        }
        std::cout << '\n';
    }
    std::cout << '\n';
    // элементы на диагонале обладают равными индексами (см. иллюстрации выше)
    for (size_t i = 0; i < std::min(n, m); ++i) {
        std::cout << matrix[i][i] << ' ';
    }
    std::cout << '\n';
}

Вывод программы выше, если будет введена квадратная матрица из примера выше:

1 2 3
4 5 6
7 8 9

1 5 9

Напишем функцию, которая будет получать по константной ссылке двумерный вектор чисел и возвращать наибольшее значение. Главное, что здесь нужно отметить – перебор всех элементов почти не изменился от того, что было рассмотрено в прошлых главах.

#include <iostream>
#include <vector>

int findMaxValue(const std::vector<std::vector<int>>& matrix) {
    int maxValue = matrix[0][0];
    // во время изучения рекомендуется явно писать даже сложные типы и не использовать тип auto
    for (const std::vector<int>& row : matrix) {
        for (const int& num : row) {
            if (num > maxValue) {
                maxValue = num;
            }
        }
    }
    return maxValue;
}

int main() {
    std::vector<std::vector<int>> matrix = {{1, 5, 3}, {8, 2, 6}, {4, 9, 7}};

    int maxVal = findMaxValue(matrix);
    std::cout << maxVal << '\n';  // 9
}

Можно аналогично реализовать функцию поиск наибольшего значения в двумерном векторе с использование обращения по индексу:

int findMaxValue(const std::vector<std::vector<int>>& matrix) {
    int maxValue = matrix[0][0];
    for (size_t i = 0; i < matrix.size(); ++i) {
        for (size_t j = 0; j < matrix[i].size(); j++) {
            if (matrix[i][j] > maxValue) {
                maxValue = matrix[i][j];
            }
        }
    }

    return maxValue;
}

В домашнем задании буду задачи на обход двумерных векторов для поиска максимального значения при соблюдении разных условий

Структуры

Часто, особенно в больших программах, может возникнуть желание объединить набор переменных не только логически, но и в коде: например, единым названием некого объекта. Структуры позволяют объединять переменные и создавать новые “составные” типы.

Создадим структуру, которая будет хранить информацию о человеке, его:

• имя

• рост

• возраст

• флаг, был ли он отчислен из университета

#include <iostream>
#include <vector>
#include <string>

struct Person {
    std::string name;  // Имя
    int height;        // Рост в сантиметрах
    int age;           // Возраст
    bool expelled;     // Флаг: был ли отчислен из университета
};

int main() {
    Person person1;
    person1.name = "Алексей";
    person1.height = 180;
    person1.age = 22;
    person1.expelled = false;

    Person person2{"Мария", 165, 20, true};

    Person person3 = {"Иван", 175, 23, false};

    Person person4{"Екатерина", 170, 21, false};
    Person person5{"Петр", 185, 24, true};

    // Создаём вектор людей
    std::vector<Person> people = {person1, person2, person3, person4, person5};

    // Выводим информацию обо всех людях в векторе
    std::cout << "Информация о людях:\n";
    for (const Person& person : people) {
        std::cout << "Имя: " << person.name << "\n"
                  << "Рост: " << person.height << " см\n"
                  << "Возраст: " << person.age << " лет\n"
                  << "Отчислен из университета: ";

        if (person.expelled) {
            std::cout << "Да";
        } else {
            std::cout << "Нет";
        }
        std::cout << "\n" << "---------------------------\n";
    }

    return 0;
}

Вывод такой программы:

Информация о людях:
Имя: Алексей
Рост: 180 см
Возраст: 22 лет
Отчислен из университета: Нет
---------------------------
Имя: Мария
Рост: 165 см
Возраст: 20 лет
Отчислен из университета: Да
---------------------------
Имя: Иван
Рост: 175 см
Возраст: 23 лет
Отчислен из университета: Нет
---------------------------
Имя: Екатерина
Рост: 170 см
Возраст: 21 лет
Отчислен из университета: Нет
---------------------------
Имя: Петр
Рост: 185 см
Возраст: 24 лет
Отчислен из университета: Да
---------------------------

Точка как структура

Рассмотрим точки в трехмерном пространстве, то есть тройки вещественных чисел \((x, y, z)\). Напишем 2 функции:

• нахождение расстояния между двумя точками

• нахождение ближайшей точки из динамического массива std::vector

\(p(p_1, p_2) = \sqrt{(x_1 - x_0)^2 + (y_1 - y_0)^2 + (z_1 - z_0)^2}\)

#include <iostream>
#include <vector>
#include <cmath>
#include <limits>

struct Point {
    double x = 0.0;
    double y = 0.0;
    double z = 0.0;
};

double getDistance(const Point& first, const Point& second) {
    double sq_disatnce = std::pow(first.x - second.x, 2) + std::pow(first.y - second.y, 2)
                         + std::pow(first.z - second.z, 2);
    return std::sqrt(sq_disatnce);
}

Point findClosestPoint(const Point& target, const std::vector<Point>& points) {
    Point closest_point = points[0];
    double minDistance = getDistance(closest_point, target);

    for (const Point& point : points) {
        double distance = getDistance(point, target);
        if (distance < minDistance) {
            minDistance = distance;
            closest_point = point;
        }
    }
    return closest_point;
}

int main() {
    // Определим несколько точек
    Point p1(1.0, 2.0, 3.0);
    Point p2(4.0, 5.0, 6.0);
    Point p3(7.0, 8.0, 9.0);
    Point p4(2.0, 2.0, 2.0);
    std::vector<Point> points = {p1, p2, p3};

    double dist = getDistance(p1, p2);
    std::cout << "Расстояние между p1 и p2: " << dist << '\n';

    // Найдём ближайшую точку к p4 из вектора
    Point closest = findClosestPoint(p4, points);
    std::cout << "Ближайшая точка к p4: (" << closest.x << ", " << closest.y << ", " << closest.z
              << ")\n";
}

Расстояние между p1 и p2: 5.19615
Ближайшая точка к p4: (1, 2, 3)

Выравнивание структур

Сумма размеров полей структуры не всегда совпадет с настоящим ее размером. Например, следующие структуры будут иметь одинаковый размер:

#include <iostream>

struct TestStruct1 {
    double a;
    double b;
};

struct TestStruct2 {
    double a;
    char b;
};

int main() {
    std::cout << sizeof(TestStruct1) << '\n';  // 16 = 8 + 8
    std::cout << sizeof(TestStruct2) << '\n';  // 16 != 8 + 1
}

Процессору быстрее и проще читать “выравненные” (“aligned”) адреса в памяти – те, которые делятся на 4 (реже – на 8). В случае структур процессору проще отсчитывать размеры наибольшего поля в структуре (в нашем случае double). То есть компилятор применяет выравние структуры (structure alignment), добавляя лишние невидимые байты между полями

В действительности TestStruct2 будет дополнена тремя байтами выравнивания и сохранится как:

struct TestStruct2 {
    double a;
    char b;
    // или проще char gap[7]; но мы не смотрели такие массивы
    char n1;
    char n2;
    char n3;
    char n4;
    char n5;
    char n6;
    char n7;
};

К добавленным полям выравнивания нельзя получить доступ по имени (у них его нет).

Более сложный случай выравнивания:

struct TestStruct1 { // 24 байта
    char a;
    int b;
    char c;
    double d;
};

struct TestStruct1 { // 24 байта
    char a;
    char gap_1[3];
    int b;
    char c;
    char gap_2[7];
    double d;
};

struct TestStruct1 { // 16 байта
    double d;
    int b;
    char c;
    char a;
};

Последний пример иллюстрирует, что аккуратная перестановка полей структуры позволяет иногда экономить память на выравнивании полей.