Оценка сложности алгоритмов и простые числа

Оценка сложности алгоритмов

Чтобы оценить, насколько “сложной” для компьютера будет программа, насколько долго он будет ее считать, замерить время в секундах недостаточно: разные компьютеры обладают разной производительностью. Более того, время исполнения программы зависит от входных данных. Мы решим эту проблему подсчетом количества операций, которые наша программа будет совершать

Упрощенная модель

За 1 операцию будем считать:

арифметические операции (битовые операции тоже)
любое обращение к памяти (считаем, что все лежит в идеальной бесконечной RAM, из которой можно получить данные моментально)
доступ к элементу вектора

Модель действительно упрощена, ведь в реальном мире на все требуется реальное время, а память компьютера является неоднородной. Регистры процессора, L1-кэш, RAM, HDD/SDD – все это разная память с разными возможностями, но мы не будем их рассматривать, также как и случаи слишком больших данных (например, когда массив, который нужно обработать, невозможно полностью загрузить в RAM).

Подробнее о времени разных операций

O-нотация

Для каждого алгоритма можно посчитать количество операций, оно будет зависеть от входных данных. Введем удобные обозначения для неточного восприятия функций

\(f(x) = {\cal{O}}(g(x)) \stackrel{def}{\Leftrightarrow} \exists C > 0: f(x) < C \cdot g(x)\)

Во всех дальнейших рассуждениях мы будем рассматривать все равенства и неравенства при больших \(x\) (более формально, \(x \to +\infty\)) и говорить об асимптотическом стремлении.

Такая запись позволяет легко определить рост функции: линейный, квадратичный, кубический, экспоненциальный, потому что только функций одной скорости асимтотического роста будет соблюдаться определение выше.

Пусть \(x \to +\infty\), тогда:

\(f(x) = x^3 + 2x^2 - 3x + 2 < x^3 + 2x^3 + 3x^3 + 2x^3 = 8x^3 \Rightarrow C = 8 > 0 \\ f(x) = x^3 + 2x^2 - 3x + 2 = {\cal{O}}(x^3)\)

График одинакового роста функций при больших x

Несмотря на то что \(x^3\) меньше, чем \(f(x)\), нашелся константный множитель, с которым можно оценить нашу функцию \(f(x) < 8x^3\). Значит, рост кубический.

Рассмотрим на примерах:

Для большей связи с дальнейшим приложением можно считать, что функции подсчитывают количество операций, которые совершит наша программа.

\(f_1(n) = 1 + 2 + \dots + n = \frac{n(n + 1)}{2} = \frac{n^2}{2} + \frac{n}{2} < \frac{n^2}{2} + \frac{n^2}{2} = n^2 \Rightarrow f_1(n) = O(n^2)\)

\(f_2(n) = 1^2 + 2^2 + \dots + n^2 = \frac{n(n + 1)(2n + 1)}{6} = O(n^3)\)

Сложность пройденных задач

Разность между наибольшим и наименьшим значениями

За какую сложность можно найти разность между наибольшим и наименьшим значениями в некотором массиве из \(n\) элементов? Нам придется пройтись по всем элементам массива и на каждой итерации обновлять минимум и максимум. Главное, что мы будем знать их после такого прохода и сможем найти сумму. Это линейная сложность – \(O(n)\).

Покажем это более формально

#include <iostream>
#include <algorithm>
#include <vector>

int main() {
    std::vector<int> data = {1, 2, 5, 2, 3, 1, -1, 5, 2, 1};
    int max = data[0], min = data[0];
    for (size_t i = 0; i < data.size(); ++i) {
        max = std::max(max, data[i]);
        min = std::min(min, data[i]);
    }

    printf("%d\n", max - min);
}

На каждой итерации циклы мы проведем 2 сравнения, возможно, 1 присваивание. После цикла вычитание и вывод на экран. Покажем, почему такой мелкий подсчет количества операций неважен при обсуждении асимптотической сложности программы:

\(n \cdot (2 + 1) + 1 = 3n + 1 < 5n < 10n < 10^6 n = O(n)\)

При O-нотации мы можем опускать константы (см. формальное определение выше), а также не учитывать вклад младших степень – ведь он будет незначителен при “достаточно большом” \(n\) (\(n \to + \infty\))

Таким образом, программа выше обладает линейной сложность.

Количество единиц в двоичной записи

Какова сложность поиска всех цифр числа в двоичной записи? Например, какова сложность подсчета количества единиц?

Для этого вспомним код для такой задачи:

#include <iostream>

int main() {
    int num;
    std::cin >> num;

    int cnt = 0;
    while (num) {
        cnt += num % 2;
        num /= 2;
    }
    std::cout << cnt << '\n';
}

Заметим, что на каждой итерации цикла число num уменьшает в 2 раза. В целых числах это можно сделать не более \(\log_2 n\) раз. Значит, наш алгоритм обладает логарифмической сложностью: \(O(\log n)\)

Стоит обратить внимание, что при указании асимптотической сложности нет смысла указывать основания логарифма, ведь рост любой логарифмической функции одинаков при больших \(n\). Это объясняется тем, что все логарифмы можно привести к одному основания умножение на константу, что там не важно по определению O-нотации

\(f_a(x) = \log_a x = \frac{\log_2 x}{\log_2 a} = \frac{1}{\log_2 a} \cdot \log_2 x = C \cdot \log_2 x = {\cal{O}}(\log x)\)

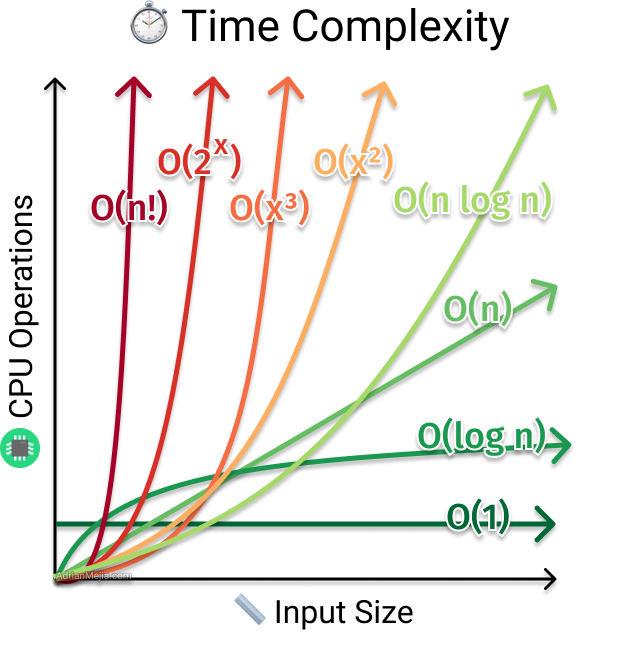
Какие сложности могут встретиться?

Сложности перечислены в порядке возрастания:

\({\cal{O}}(1)\) – константная сложность, то есть количество операций не зависит от входных данных
\({\cal{O}}(\log n)\) – логарифмическая сложность
\({\cal{O}}(\sqrt n)\)
\({\cal{O}}(n)\) – линейная сложность, “линия” – количество операций не более чем прямо пропорционально входным данным
\({\cal{O}}(n \log n)\) – квазилинейная сложность
\({\cal{O}}(n^2)\) – квадратичная, кубическая сложность. Здесь же будут все \({\cal{O}}(n^a)\), где \(a\) – это параметр
\({\cal{O}}(2^n)\) – экспоненциальная сложность. Здесь же будут все \({\cal{O}}(a^n)\), где \(a\) – это параметр
\({\cal{O}}(n!)\) – факториальная сложность

Быстрое возведение в степень

Наивный алгоритм возведение в степень будет работать за \(O(n)\): \(n\) раз нужно умножить на число.

Заметим, что:

\[ n \ \vdots \ 2 \Rightarrow a^n = a^{\frac{n}{2}} \cdot a^{\frac{n}{2}}, \text{где} \ \frac{n}{2} \in \mathbb{Z} \\ n \not{\vdots} \ 2 \Rightarrow a^n = a^{n - 1} \cdot a \]

Теперь напишем псевдокод для быстрого возведения числа num в степень deg. Будем считать, что все переменные корректно объявлены заранее

result = 1

пока deg != 0:
    если deg четное, то
        deg = deg / 2    # уменьшаем степень, в которую остально возвести, в 2 раза
        num *= num       # возводим текущее число в квадрат
    если deg нечетно, то
        deg -= 1
        result *= num # умножаем на основание степени, на исходное число

теперь в result лежит num в степени deg

Для расчета асимптотической сложности заметим, что:

после обработки нечетного deg, оно становится четным и на следующей итерации будет разделено на 2
deg уменьшается в 2 раза при каждом делении, а это, как мы уже знаем, может происходить не более \(\log_2 d\) раз

Тогда нашу сложность можно выразить как \(\log d + \log d\) = \(O(\log d)\) – логарифмическая сложность

Простые числа

Число называется простым, если не имеет делителей, кроме 1 и себя.

Известно, что для любого натурального числа существует и единственно разложение на простые множители.

Нам предстоит научиться проверять число на простоту, раскладывать число на простые множители и вывести сложность этих алгоритмов.

Парные делители

Если \(n \ \vdots \ a\), то \(b := \frac{n}{a} \in \mathbb{N}\). Очевидно, что \(ab = n\). Будем называть такую пару \(a\) и \(b\) парными делителями.

Лемма. Один из них меньше корня, а другой – больше.

Предположим, что это не так, тогда: dfss \[ \left[ \begin{gathered} \ \begin{cases} a < \sqrt n \\ b < \sqrt n \\ \end{cases} \Rightarrow ab < n - \text{противоречие c } n = ab \\ \begin{cases} a > \sqrt n \\ b > \sqrt n \\ \end{cases} \Rightarrow ab > n - \text{противоречие с } n = ab \ \end{gathered} \right. \]

Значит, наше предположение неверно, лемма доказана. Действительно, один из парных делителей меньше корня, другой – больше.

Проверка числа на простоту

Чтобы проверить, является ли число простым, достаточно проверить все числа до корня из этого числа и убедиться, что среди них нет делителей.

for a: 2 -> sqrt(n)
   if n делится на a => n - составное число

if все итерации выполнены, а условие в цикле так и не сработало, то
    n - простое число

Перебор всех делителей числа

Для получения всех делителей числа достаточно перебрать все делители до корня и для каждого найденного найти парный делитель. Так мы получим множество всех делителей: как меньших корня, так и больших.

Приведем идею в формате псевдокода на примере подсчета всех четных делителей:

cnt = 0
for a: 2 -> sqrt(n)
   if n делится на a, то
      b = n / a # тоже целое число, так как мы в условии, что n делится на a
      # a и b -- наши парные делители
      if a делится на 2 => cnt += 1
      if b делится на 2 => cnt += 1
      if a == b and a делится на 2 => cnt -= 1

cnt - количество четных делителей

Несколько примеров, почему условия написаны именно так:

нельзя использовать else if, так как возможен вариант \(a = 2, b = 8, n = 16\), то есть \(b\) четное при четности \(a\)
необходима проверка if a == b => cnt -= 1 на тот случай, если число является точным квадратом, потому что тогда мы дойдем до корня, который будет целым числом. Пример: \(a = 4, b = 4, n = 16\). В этом случае мы прибавим единицу 2 раза (в каждом из условий), но ведь числа \(a\) и \(b\) равны, и их нужно считать 1 раз. Решаем эту проблему вычитанием “лишней” единицы при условии a == b

Факторизация числа

Факторизация – разложение на простые множители. Это возможно сделать для любого числа (см. теорему выше). Приведем алгоритм, который будет работать за \(O(\sqrt n)\) и сохранять все делители в std::vector. Важно отметить, что рассматривается не самая оптимальная по использованию памяти версия, ведь если \(n \ \vdots \ 2^k\), то мы добавим \(2\) в вектор \(k\) раз. Для более аккуратного подсчета степеней у нас пока нет достаточных знаний: в недалеком будущем мы начнем активнее использовать библиотеку STL и, возможно, рассмотрим более оптимальную по использованию памяти модификацию. Асимптотика алгоритма по времени останется прежней

Идея приведенного алгоритма заключается в следующем:

ищем делитель до корня
делим на него число \(n\), пока это возможно. При каждом делении добавляем делитель в std::vector
затем продолжаем поиск делителей до корня из измененного \(n\). Действительно, все меньшие делители уже были нами рассмотрены (поэтому не изменяем счетчик цикла, не начинаем его снова с 2). Также нет смысла перебирать делители, которые больше корня из разделенного \(n\) – поэтому идем до \(\sqrt n\)
после завершения этого цикла мы точно нашли все делители числа \(n\) и на все из них поделили. Значит, после нашего цикла \(n = 1\). Единственное исключение – когда \(n\) само было простым, ведь тогда мы не нашли делители и не добавили в вектор. Проверим это после основного цикла

data = {}
for a: 2 -> sqrt(n)
    while n делится на a
        добавить делитель a в массив data
        n = n / a # делим на найденный делитель

if n != 1, то # n было простым
    добавить a в массив data

data содержит все делители

Сортировка std::vector

Если мы добавили все простые делители в std::vector, то затем нам может потребоваться отсортировать этот массив в порядке возрастания. Сделать это можно с помощью функции sort из стандартной библиотеке

#include <iostream>
#include <algorithm>
#include <vector>

int main() {
    std::vector<int> data = {1, 5, 2, 4, 3};

    std::sort(data.begin(), data.end()); // теперь вектор отсортирован
    // data равняется {1, 2, 3, 4, 5}

    for (int elem: data) {
        std::cout << elem << ' ';
    }
    // будет выведено: 1 2 3 4 5
    std::cout << '\n';
}