Сортировки. Компараторы

Пришла пора начать новый раздел и рассмотреть следующие рассмотреть более прикладное применения программирования: для численного решения различных задач поиска, а также для проведения геометрических расчетов и обработок геометрических объектов.

В этой главе нам предстоит научиться находиться нули и экстремумы функций с заданной точностью, а также примерную длину кривой.

Численные методы

Существует множество математических объектов, задач, конструкций, которые позволяют проводить анализ теоретических объектов и получать математически правильный ответ. В математике, например, существует известное вами число \(\pi\) – оно является трансцендентным, то есть представим исключительно как бесконечная непериодическая десятичная дробь. С этим числом можно проводить расчеты, писать его в ответ. Другим примером трансцендентного числа является число \(e\), которое, как правило, определяется как предел последовательности \(e := \lim_{n \to \infty} (1 + \frac{1}{n})^n\) или как сумма бесконечного ряда: \(e:= \sum_{n = 0}^{\infty} \frac{1}{n!}\). Интегралы – площадь под графиком функции. Дифференциал дифференцируемой функции всегда существует

Это все корректно определенные математические понятия, но в прикладных задачах реализовать и использовать бесконечность невозможно. Понятно, что для практических задач достаточно знать число \(\pi\) с конечной и весьма небольшой точностью. Нам не обязательно знать, что корнем уравнения является \(\frac{1 + 2 \sqrt 5}{3}\), достаточно понимать, что это \(\frac{1 + 2 \sqrt 5}{3} \approx 1.824045318333193\)

Численные методы – это совокупность приемов, которые позволяют реализовывать математические опередения за конечное количество операций с числами. Часто это включает учет машинной точности, приближенное решение задач, алгоритмические приемы в решении уравнений, например. В этой главе мы познакомимся с некоторыми базовыми алгоритмами.

Нули функции методом половинного деления

Как известно из уроков математики, нули функции \(f(x)\) – корни уравнения \(f(x) = 0\). Разобьем область опередения фунции на отрезки, в каждом из которых находится ровно один нуль функции (он также не совпадает с границами выделенных отрезков). Математически:

\[ D(f) = [a_1; a_2] \cup [a_2; a_3] \cup \dots \\ \ \\ \forall i \ \exists ! \ x \in [a_i; a_{i + 1}] : f(x) = 0 \]

Постановка задачи: построим алгоритм, которые позволит искать с точностью \(\varepsilon\) нуль функции \(f\) на отрезке \([a; b]\), если известно, что в этом отрезке содержится ровно один нуль функции (\(x_0 : f(x_0) = 0\)). То есть будем искать такое \(x_*\), что \(|x_* - x_0| < \varepsilon\).

  • \(m := \frac{a + b}{2}\) – середина отрезка

  • если \(f(a) < 0\), то есть если функция меняет знак с \(-\) на \(+\), см. график справа

    • \(f(m) \ge 0 \Rightarrow x_0 \in [a; m]\), то есть стягиваем правую границу отрезка: \(b = m\)

    • \(f(m) < 0 \Rightarrow x_0 \in [m; b]\), то есть стягиваем правую границу отрезка: \(a = m\)

  • если \(f(a) > 0\), то есть если функция меняет знак с \(+\) на \(-\)

    • \(f(m) \ge 0 \Rightarrow x_0 \in [m; b]\), то есть стягиваем правую границу отрезка: \(a = m\)

    • \(f(m) < 0 \Rightarrow x_0 \in [a; m]\), то есть стягиваем правую границу отрезка: \(b = m\)

  • повторяем пункты выше, пока \(|b - a| > \varepsilon\)

  • затем \(x_* = \frac{a' + b'}{2}\) – середина итогового отрезка

image.png

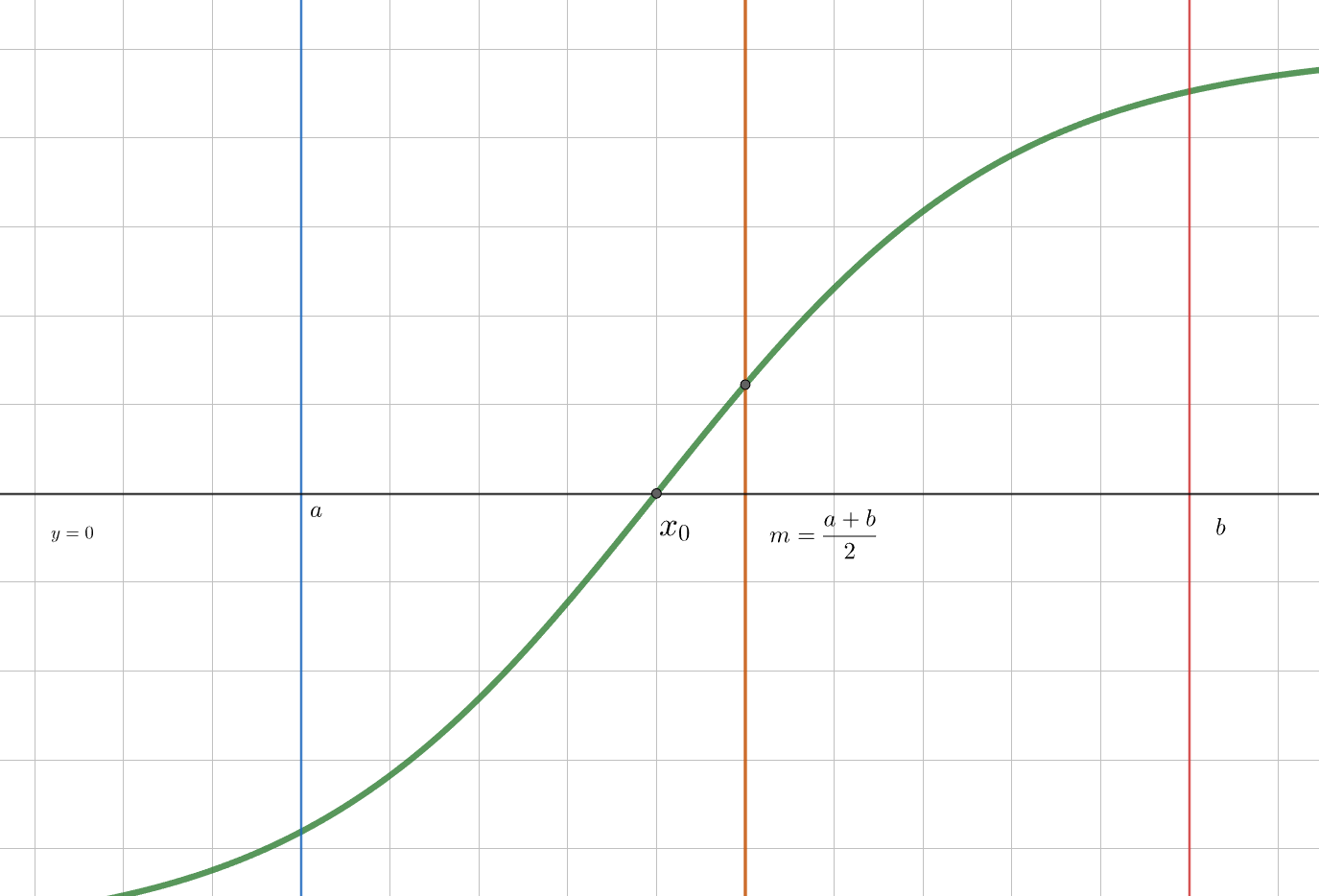
Заметим, что точка \(m\) по построению делит отрезок \([a; b]\) пополам, значит, каждая итерация уменьшает рассматриваемую область в 2 раза. Рассчитаем сложность алгоритма.

\(L_k = b_k - a_k\) – размер отрезка поиска после \(k\)-той итерации

\[ \begin{gathered} L_k = b_k - a_k \text{- размер отрезка поиска после k-той итерации} \\ \ \\ L_k = \frac{1}{2} L_{k - 1} = \left( \frac{1}{2} \right)^k L_0 \\ \ \\ \ \frac{\varepsilon}{2} \le L_n \le \varepsilon \\ \ \\ \frac{\varepsilon}{2} \le \left( \frac{1}{2} \right)^k L_0 \le \varepsilon \\ \ \\ \frac{\varepsilon}{2 L_0} \le \left( \frac{1}{2} \right)^n \le \frac{\varepsilon}{L_0} \\ \ \\ \ \log_{(\frac{1}{2})} \frac{\varepsilon}{2 L_0} \ge n \ge \log_{(\frac{1}{2})} \frac{\varepsilon}{L_0} \\ \ \\ \ \log_{2} \frac{2 L_0}{\varepsilon} \ge n \ge \log_{2} \frac{L_0}{\varepsilon} \\ \ \\ \ \log_{2} \frac{L_0}{\varepsilon} \le n \le 1 + \log_{2} \frac{L_0}{\varepsilon} \Rightarrow n = {\cal{O}} \left( \log \frac{L_0}{\varepsilon} \right) = {\cal{O}} \left( \log \frac{b - a}{\varepsilon} \right) \end{gathered} \]

Таким образом, алгоритм имеет логарифмическую сложность и гарантирует, что для любой точности \(\varepsilon\) найдется приближенный корень.

Также метод половинного деления называют методом дихотомии или методом бисекции.

Экстремумы функции методом половинного деления

Унимодальная функция имеет ровно 1 экстремум (минимум или максимум). Мы будем рассматривать унимодальные на отрезке функции – те, которые на данном отрезке имеют ровно один экстремум.

Экстремум функции – это такая точка, в некоторой окрестности которой все значения функции больше (или меньше) значения в этой точке. То есть если брать точки, близкие к точке максимума, то значения фукнции в них будет меньше. Более формально:

\[ x_0 - \operatorname{max} \stackrel{\text{def}}{\Leftrightarrow} \exists \varepsilon > 0: \forall x \in [x_0 - \varepsilon; x_0 + \varepsilon] : f(x) < f(x_0) \]

Аналогично можно записать определение для минимума функции.

Теперь применим уже знакомый нам алгоритм для поиска экстремума. Рассмотрим на примере максимума.

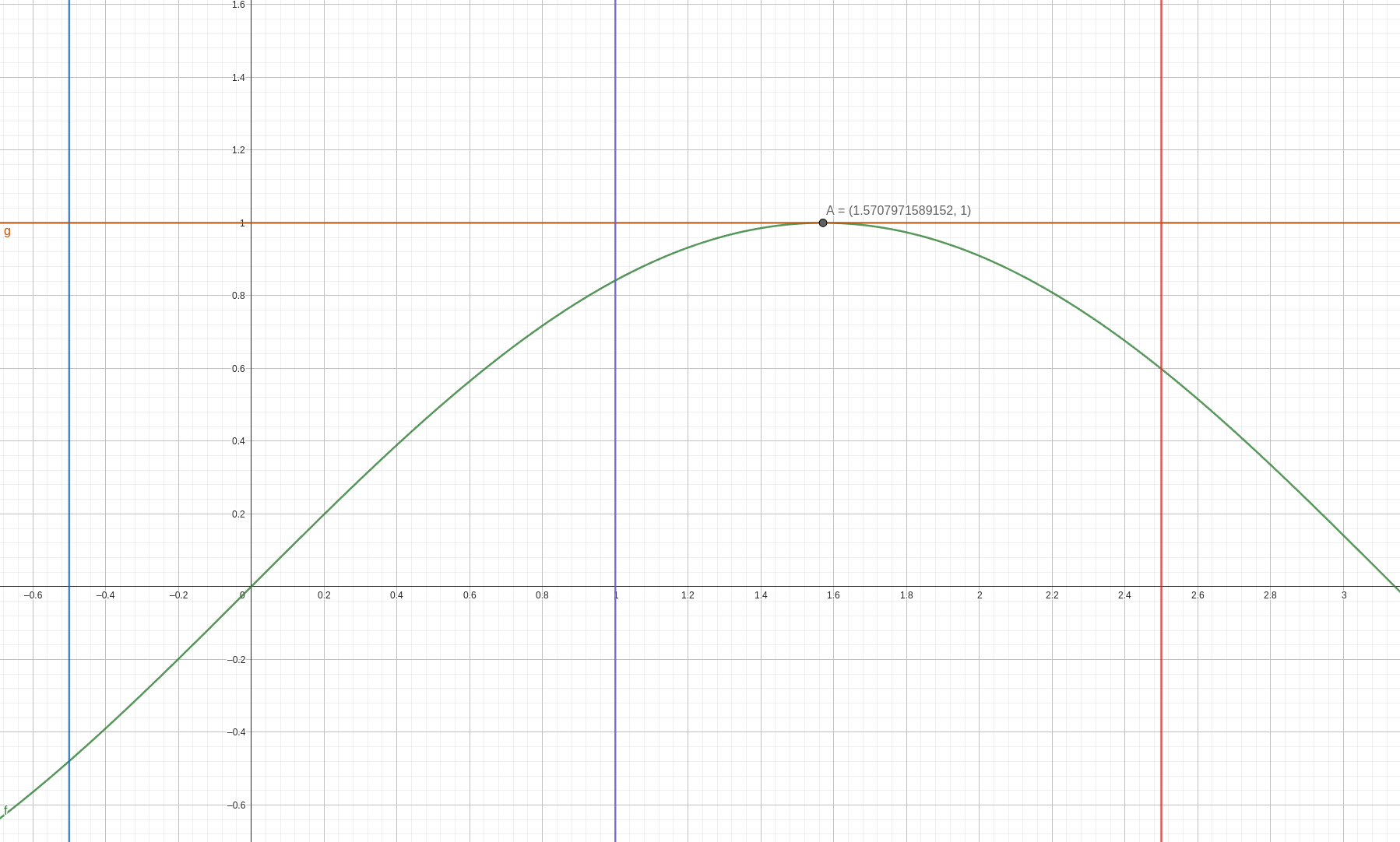Здесь показана унимодальная на отрезке функция, границы отрезка и выбранно значение m Здесь показана унимодальная на отрезке функция, границы отрезка и выбранно значение \(m\)

Заметим, что в случае максимума функция возрастает до точки максимума и убывает после нее.

  • \(m := \frac{a + b}{2}\) – середина отрезка

  • \(x_1 := m - \delta\), \(\ \ \ x_2 := m + \delta\), \(\delta \approx 10^{-5}\) – выбираем 2 точки, очень близкие к середине

  • если \(f(x_1) < f(x_2)\), то есть если функция возрастает в окрестности середины, то середина находится слева от точки максимума

    • \(x_{max} \in [x_1; b]\), то есть стягиваем правую границу отрезка: \(a = x_1\)

  • если \(f(x_1) > f(x_2)\), то есть если функция убывание в окрестности середины, то середина находится справа от точки максимума

    • \(x_{max} \in [a; x_2]\), то есть стягиваем правую границу отрезка: \(b = x_2\)

  • повторяем пункты выше, пока \(|b - a| > \varepsilon\)

  • затем \(x_{max} = \frac{a' + b'}{2}\) – середина итогового отрезка

По сути все, что поменялось – метрика, по которой мы выбираем левую или правую половину отрезка. Поскольку \(\delta\) выбирается малой, на каждой итерации длина рассматриваемого отрезка сокращается в 2 раза, поэтому асимптотика сохраняется.

Площадь под графиком

Идея: приблизить функцию линейными функциями на каждом из малых отрезков. Площадь на отрезке под прямой можно легко найти.

Иллюстрация: https://www.geogebra.org/calculator/cxwmudtz